Loudspeaker Thiele/Small Parameter Extraction

Here we extract basic free air Theile/Small parameters from the complex impedance curve of a 10” low frequency driver. These parameters may be used to verify the manufacturers published specifications and provide the basis for enclosure design.

Two external resistors are required to perform this measurement. First a resistor (R1), to establish a constant current in the circuit is required. The precision and value of this resistor is not critical. However, if it is too low (< 30Ω), its purpose is defeated and if it is too high (> 5kΩ) noise immunity of the circuit will be compromised.  Secondly a precision reference resistor (R2), whose value is known to two decimal points, is required. This provides the software with a known reference so that it can accurately plot the absolute value of the driver impedance in the spectrum analyzer.

We will use "32768_MLS_Impedance_Measurement.process" to perform the measurement. This process ships with the release version of this product. It consists of four modules. The first is the signal generator, which generates a 32768 length MLS stimulus to excite the DUT. Second is the SoundIO module, which plays the stimulus and records the response of the driver. Third is the Oscilloscope module, which allows us to view the time domain response of the driver. Finally is the Spectrum Analyzer, which performs an FHT/ FFT on the time domain data and allows us to view impedance vs. frequency and phase vs. frequency graphs.

You must have a dual channel, duplex sound card to perform this measurement.

1.    Measure the value of the reference resistor using a precision ohmmeter or DC resistance bridge. Our reference measures in at 10.067Ω.

2.    Measure the DC resistance of the drivers voice coil (R_E) to the nearest 0.1Ω. Use a precision ohmmeter or bridge. Our voice coil measures in at 6.89Ω. This application cannot measure the DC resistance of the drivers voice coil directly. This is due to the fact that most sound cards are AC coupled, that is they have a capacitor between their internal amplifier and their output jack, and thus do not pass DC current. Driver voice coil resistance can be measured using very low frequency sine waves (< 1Hz) and a series precision resistance but most sound cards cannot reliably reproduce such frequencies. If you have a 1.5 volt battery and voltmeter available you can wire the loudspeaker and the precision resistor in series across the battery terminals and calculate the voice coil resistance using the following equations.

3.    Suspend the driver vertically about half way between the ceiling and the floor using a piece of wire or twine. Do not place the driver horizontally on a table or other reflective surface. This will result in cone pre-loading that will cause errors. Reflections from any nearby surface will cause response ripples in the impedance curve.

4.    Wire the circuit as shown in Figure 1.  Use short, low resistance or shielded wiring. Note that many sound cards speaker outputs have more swing than their respective line inputs.

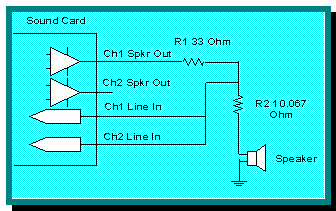
Figure 1: Thiele/Small Extraction Process Calibration Wiring

5.    If you are running Windows 7 or 8 or Vista you must disable all sound effects applied to your sound card. Right click the sound icon on the windows task bar and select Playback devices from the popup menu that appears. Select the sound card you intend to use from the "Select a playback device below to modify its settings" listbox and press the Properties button. Select the Enhancements tab and check the Disable all Sound effects checkbox. Press the OK button.

Figure 2: Windows 7/Vista Playback Enhancements Disabled

6.    Open " C:\Users\Public\Documents\Sonic Beacon\Sonic Beacon\32768_MLS_Impedance_Measurement.process" from the applications File…Open… menu. Press OK if the “No Compatible Calibration File Present” message box appears.

7.    Open the FFT Options dialog from the applications Options…FFT… menu and ensure the FFT Size is 32768. Press OK in the FFT Options dialog box. Press OK when the “No Compatible Calibration File Present” message box appears.

8.    You need to adjust the level of your selected sound card recording path. If you are running Windows 7 or 8 or Vista right click the sound icon on the windows task bar and select Recording devices from the popup menu that appears. Double click the selected sound card in the Sound dialog box Recording tab. Select the Levels tab and adjust the slider to its one-quarter setting. Press the OK button. If you are running XP or below; select the Levels tab Press the Open Mixer button the SoundIO modules Options group. Select Options… Properties… Choose your sound card from the Mixer Device and press the Recording radio button in the Adjust Volume for group. Press the OK button. Deselect all Record Control mixer paths except the Line In. Adjust the Line In mixer slider to its one-quarter setting and equalize its balance slider.

9.    You need to adjust the output level of your selected sound cards playback path. If you are running Windows 7 or 8 or Vista select the Playback tab of the Sound dialog box and double click the selected sound card. Select the Levels tab and adjust the Line In to its 25% setting. Otherwise if you are using XP or lower select Options… Properties… Press the Playback radio button in the Adjust Volume for group. Press the OK button. Mute all Playback mixer gain settings except the Volume Control and the Wave Out. Equalize the Volume Control and the Wave Out mixer balance sliders. Adjust the Volume Control and the Wave mixer sliders to their one-quarter settings.

10.  Press the applications Run button. You should be able to see the MLS sequence in the oscilloscope module as shown in Figure 3. If a SoundIO “No data in record buffer” message appears first check that your wiring conforms to Figure 1. If it is correct, increase the mixers Playback Volume Control and Wave Out sliders or Recording Line controls.

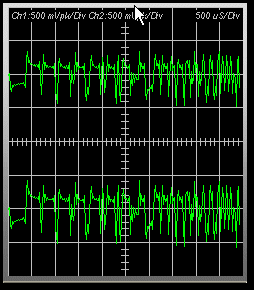
Figure 3: Thiele/Small Extraction Process MLS Sequence Setup

11.  If all three controls are at maximum you may reduce the level at which the sound card triggers. When in Record/Play mode, the SoundIO module sends a record buffer to the sound card that is 1.4 longer than required. This is to compensate for various system delays. It then scans the buffer for the first level that is greater than the trigger level. It then marks this point as the beginning of the record and returns the remainder of the record (up to the number of samples required for the selected FFT size) to the application. This is the record that the modules processes and sends to subsequent modules. Trigger level is expressed in terms of percentage full scale. Check the value in the Trig. Level (%F.S.) in the SoundIO Trigger Parameters group. If it is greater than 20 select 10 in the combo box. Press the Run button and check the oscilloscope display again. You can reduce this value to as low as 1%. This corresponds to 1% of the sound card full-scale output. You can estimate the length of the buffer that is sent to the sound card for a given FFT Size from the equation below.

If you know the full scale output voltage of your sound card, you can estimate the level that causes the SoundIO module to trigger from the equation below. Sound cards have a typical input swing ranging from +0.5 to +2.0 volts.

Once you have a valid trigger, adjust the Play Control and the Wave sliders so that the signal in the oscilloscope display is not clipped (as in Figure 3).

13.  You now need to calibrate the frequency response curve of the sound card if you do not already have a valid calibration file loaded for the input and output devices selected in the SoundIO module. Level and Latency calibration are not required for complex impedance measurement. Press the Calibration button in the SoundIO module. The SoundIO Module Calibration dialog box will open..

14.  Select Frequency from the Calibration Type Select: combo box in the Calibration Status group box. Select MLS from the Signal Type combo box in the Frequency Calibration group box.

15.  Press the Run button and wait for the Frequency Calibration Complete status message to appear. If a “No data in record buffer” message box appears Press the Open Mixer button and increase the applications output level slider. The SoundIO modules input device level may also be increased by right clicking on the Windows Task Bar Sound icon and selecting the Recording and Levels and adjusting the devices slider. Frequency calibration may be restarted by pressing the Run button. If successful, the calibration dialog should look as in Figure 4. The Calibration Progress bar may not update in certain versions of Windows.

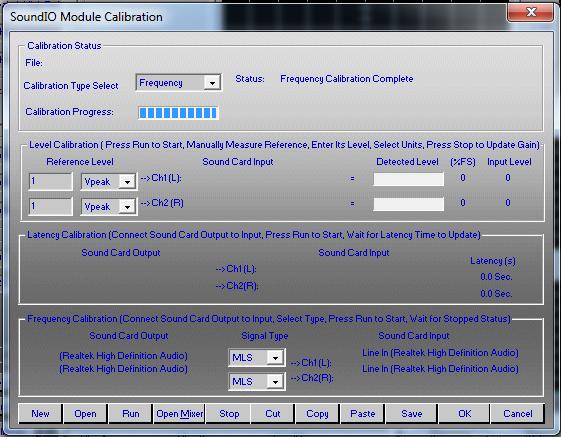
Figure 4: Thiele/Small Extraction Process Calibration Dialog after Auto Calibration

17.  Now rewire the circuit as shown in Figure 5.

Figure 5: Thiele/Small Extraction Process Test Wiring

18.  Change the Spectrum Analyzers XAxis Selection to Log10. Set the Stop Frequency to 689Hz using the Stop: Dn button in the XAxis group. Change the Y-Axis Selection and scale to |Z| and 10 ohms/div respectively. Enter the exact value of the reference resistor wired between Ch1 Line-In and Ch2 Line-In in the Ref1: edit box in the spectrum analyzer. Check the Apply Freq Cal checkbox. Change the Averaging factor to 4 in the Avg: combo box of in the spectrum analyzer. This will help smooth the low frequency results.

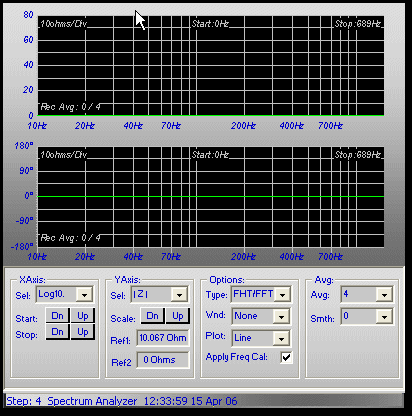
Figure 6: Thiele/Small Extraction Process Spectrum Analyzer Module Settings

19.  Press the Run button on the application toolbar and observe the trace in the spectrum analyzer. The impedance and phase appear in channels one and two respectively.

Figure 7: Thiele/Small Extraction Process Spectrum Analyzer Module With Driver Impedance and Phase Plots

20.  Find the maximum impedance in the spectrum analyzer and record it (R_max) and the frequency at which it occurred (f_SA). Pressing the right mouse button and dragging it past the impedance peak will show the driver resonant frequency and peak impedance. Our R_max = 54.93 ohms and our f_SA = 40.8 Hz.

21.  Calculate r₀ using the following equation.

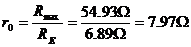
21.  Calculate Rx using the following equation. Use the markers to find the frequencies f₁ and f₂ on the impedance curve (above and below f_SA) that corresponds exactly to the impedance value of R_X. Our frequencies are f₁ = 32.9Hz and f₂ = 50.7Hz respectively.

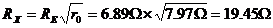
22.  Check that the square roots of the product of the frequencies (f1 and f2) are within 1 Hz of the measured f_SA. Use the following equation.

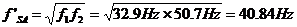
23.  Now calculate the mechanical Q of the driver at its free air resonant frequency (Q_MS) as follows:

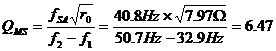
24.  Now calculate the electrical Q of the driver at its free air resonant frequency (Q_ES) as follows:

25.  Now calculate the total Q of the driver at its free air resonant frequency (Q_TS) as follows:

Below is a table showing the measured and calculated Thiele/Small parameters using two methods. First the constant current method above (column 2) and second the voltage divider method (see setup in Figure 8) using three different values of reference resistance (columns 3 to 5). They are 10.07Ω, 100.77Ω and 994.43Ω respectively. When using the Voltage Divider method accuracy depends strongly upon the assumption that R_REF is much larger than the driver impedance. As can be seen from Table 1 the measured value of the driver peak impedance at its resonant frequency (R_max) decreases as the value of R_REF increases. Hence the calculated values of Q_MS, Q_ES and Q_T (which are inversely proportional to R_MAX) will decrease as R_REF increases.

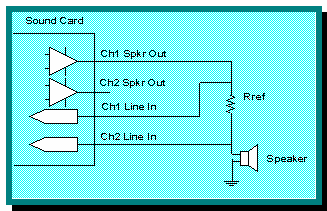
Figure 8: Thiele/Small Extraction Process Voltage Divider Method Test Wiring

Table 1: Thiele/Small Extraction Process Constant Current Verses Voltage Divider Method Test Results

21.  Now add a mass (such as back to back ceramic disk magnets or blobs of silly putty or talc) symmetrically about the cone apex. This will lower the drivers resonant frequency by increasing its cone mass. The resonant frequency of the driver must be lowered by at least 25% in order for this to work. In our case this would be a reduction of about 10 Hz. Press the Run button on the application toolbar and observe the trace in the spectrum analyzer. If the resonant frequency is not lowered by about 25% add more mass and repeat. Never add a mass greater than the cone mass. Remove the mass and weigh it to 0.1gram accuracy. You will need a good scale to do this. The total mass of our silly putty is 13.50 grams Note that paper cones may be damaged when removing silly putty. Notice the response ripples in the curves due to cone interaction with the added mass. The better distributed the mass the lower amplitude of the ripples.

Figure 9: Impedance and Phase Plots of Driver with Added Mass

22.  Find the drivers new resonant frequency on the added mass impedance curve. Ours is now about 31.1Hz. Then compute the mechanical mass of the driver cone assembly (including air load) (M_MS in kilograms) as follows:

23.  The mechanical compliance of a drivers suspension is the inverse of how much force (Force = mass x acceleration) it takes to push the cone per unit distance (per meter). The lower the compliance the harder it is to push the cone back into the drivers’ magnetic assembly. Compliance is inversely proportional to drivers’ cone mass and it free air resonant frequency. This makes sense because the greater a given mass, the lower its resonant frequency and the harder it is to push around. Compute the drivers mechanical compliance (C_MS) as follows:

30.  Measure the driver cone effective surface area (S_D in meters²). Measure the diameter of the driver cone including one half of the surround. Ours is a 10” driver so our effective diameter is about 8.25”. Thus our radius (effective diameter / 2) is 4.125”. Converting to metric we get 4.125” x 1m / 39.37” = 0.105m. Thus:

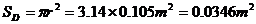
29.  The free air resonant frequency of a driver is inversely proportional to the square root of its compliance and its total mass. This mass includes the mass of the cone, the voice coil assembly, the dust cap and about half of the surround and spider. The surrounding air has mass as well and so it exerts a pressure on the cone. This lowers the resonant frequency. The mass is proportional to air density (p = 1.18kg/m3 @ 20C @ sea level) and the radius of the cone (0.105m). It ranges from 0.001kg for a 3" driver to about 0.027kg for an 18" driver.  When the driver is suspended in free air this effective mass (M_M1) can be calculated as follows.

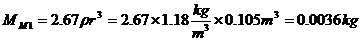
30.  The mass of the driver cone assembly(M_MD) excluding air load is:

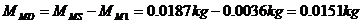
31.  We can now check the free air driver resonant frequency (f_SA). The result is very close to our measured value of 40.8Hz.

32.  A driver in an enclosed box is a piston pushing against a volume of compressible air. The larger the cone and the smaller the air volume the harder it is for the cone to move back and forth against the enclosed volume of air. The enclosed volume of air that has the same stiffness as the driver’s suspension system when compressed by a piston the same diameter as the driver cone is known as V_AS.  It is usually measured in manufacturer’s data sheets as liters of air at standard temperature (20C) and pressure (sea level). However 1 liter of air at standard temperature and pressure occupies 1000 liters The volume of air having the same acoustic compliance as the driver suspension (V_AS in meters³) is calculated as follows:

where: p = the density of air (1.18 kg/m³  at 20°C @ sea level)

and: c = speed of sound (344.5 m/s at 20°C @ sea level)

33.  From these basic parameters we can determine an enclosure type (baffle, closed or vented box). Calculating the drivers Efficiency Band-width Product (EBP) will give us an idea of the type of enclosure to design. If the EBP is less than 50 a sealed enclosure might be more suitable. If greater a vented enclosure should be designed. As can be seen our driver should go into a closed box.

34.  When a driver is placed in a closed box it behaves like another driver with a heavier cone and a stiffer suspension. Its resonant frequency is lowered and its Q is raised. In order to calculate the driver Bl product (Bl), efficiency (n₀) and power sensitivity (Sp) we need to know a little about the intended enclosure. Calculation of these parameters requires that we know the resonant frequency of the driver (f_SB) when it is mounted in the enclosure. We will design a sealed enclosure for the driver with a total system Q_TC of 1.0. This system will have warm robust lower end. The system response will be boosted by about 1.25 dB near the cut-off frequency. First we calculate system alpha as follows:

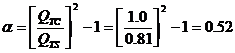
35.  The estimated system resonance may be calculated as follows:

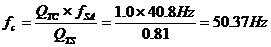
36.  The required box volume may be calculated as follows:

37.  In order to calculate the resonant frequency of the driver (f_SB) when it is mounted in the enclosure we need to know the mass reactance loading on both the front and rear of the cone. To calculate the mass reactance loading for the front of the driver cone (M_MR[front]) in a box less than 8ft³:

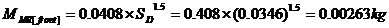
38.  The equation for the effective mass loading on the rear of the cone is

39.  To solve this equation we need to know the value of K_m For rectangular baffles K_m approximately equals:

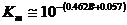
40.  To solve this equation we need to know the value of B. B is the ratio of the cone area (S_D) to the front baffle area (height x width). We will design a rectangular box with side dimensions (height, width and depth) in the ratio of 1.6:1.2:1. Thus to calculate the depth of the box from which all other dimensions can be derived from:

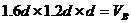
41.  Thus the ratio (B) of the cone area (S_D) to the front baffle area (h x w).

40.  So K_m equates to:

30.  So the effective mass, reactance loading on the rear of the cone (M_MR[rear]) is:

31.  In order to find the mechanical mass of the driver excluding air load (M_MD) we subtract the mass, reactance loading of the drivers piston mounted in free air (M_M1) from the total mass, reactance of the driver cone assembly including air load (M_MS)

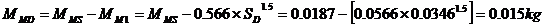
41.  Now we add the mechanical mass of the driver excluding air load (M_MD) plus the mass, reactance loading for the front of the driver cone (M_MR[front]) plus the effective mass, reactance loading on the rear of the cone (M_MR[rear]) to get the mechanical mass of the driver cone assembly excluding air load (M'_MS) when it is mounted in the box.

42.  Now we can find the resonant frequency (f_SB) and Q (Q_TB) of the driver mounted in the enclosure. Notice that the driver resonant frequency is lowered (from f_SA = 40.8 Hz to f_SB = 38.4 Hz) and its Q is raised (from Q_TS = 0.81 to Q_TB = 0.86), just as predicted.

43.  The Bl product is a measure of the driver motor strength. It is equal to the field strength of the driver magnet multiplied by the length of the voice coil wire in the field. Large, heavy cones with large excursion requirements (X_max) need strong motor systems to control harmonic distortion. As more of the voice coil moves out of the pole piece gap it takes more electrical energy to move the cone a given distance. From the corrected resonant frequency (f_SB) the Bl product (Bl) of the 10” low frequency driver may be calculated as follows:

44.  Efficiency defines how much acoustic power per electrical watt of input the driver can produce. It is used to match components in multi driver systems. Then also from the corrected resonant frequency (f_SB) the half plane, mid-band efficiency (n₀) (full-space efficiency is 3dB less) of the 10” low frequency driver may be calculated as follows:

45.  Reference power sensitivity is the sound pressure level produced by the driver when mounted on a large baffle at 1 meter with an electrical input of 1 Watt. From the corrected mid-band efficiency (n₀) the power sensitivity of the 10” low frequency driver can be calculated as follows:

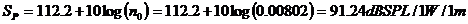
What We Do

Sonic beacon produces electrical and acoustical data acquisition and analysis software for the Windows operating system.

About Us

Sonic beacon is a Canadian organization that provides a free set of virtual instruments that are useful for measuring the time and frequency domain responses of audio components using a personal computer. It is located in Pakenham Ontario which is near Ottawa, Canada.

News and Events

March 23, 2014: 32 and 64 Bit Versions of sonic beacon (1.1.0.9) released. Tested on Microsoft Windows 8 (64 Bit), Microsoft Window 7 Home Premium (64 Bit) and Windows XP 32 Bit Professional.